|
|
|
Устойчивость ракеты в полете
Во время полета на неуправляемую ракету действуют в основном три силы: тяга двигателя R, аэродинамическая сила Р и сила тяжести Q (рис. 2.24).

Тяга ракеты направлена вдоль оси симметрии, сила тяжести в соответствии с законами механики приложена в центре тяжести (центре масс) и действует в направлении центра Земли, а аэродинамическая сила соответствует набегающему потоку ветра. Точка приложения силы Р называется центром давления. Для движения вдоль заданной траекторииракета должна быть устойчивой. Движение ракеты вдоль траектории устойчиво в том случае, когда действующие на нее силы и моменты непрерывно сохраняют равновесие и направляют ракету на первоначальную траекторию полета. На рис. 2.25 показаны три вида траекторий для случаев: а) устойчивой ракеты на траектории; б) устойчивой ракеты, на которую подействовало возмущение,затухающее под влиянием приложенных к ракете сил и моментов; в) неустойчивой ракеты, когда действующие на нее силы и моменты не в состоянии привести к затуханию все возрастающих возмущений
.
Для сохранения устойчивости тела (не только ракеты), движущегося в воздухе, его центр тяжести должен находиться впереди центра давления (считая от головной части). Это основное условие очень важно для безопасного старта и полета ракеты. Если центр тяжести будет расположен позади центра давления, то ракета, выведенная из равновесия случайным возмущением, не возвратится на первоначальную траекторию полета.
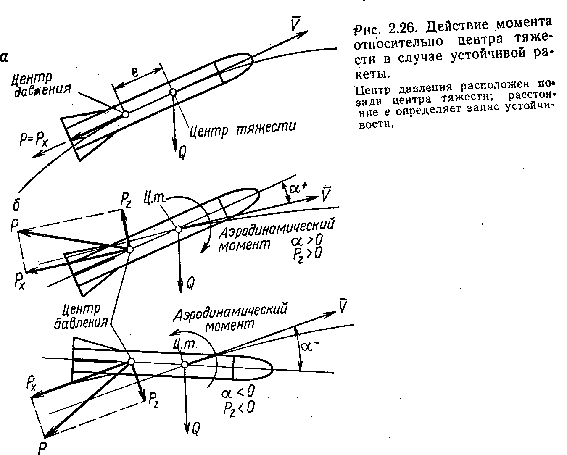
Рис. 2.26 иллюстрирует характер влияния сил и моментов на устойчивую ракету: а) при невозмущенном полете по траектории; б) при отклонении от траектории на положительный или отрицательный угол а.

На рис. 2.27 показана ракета, у которой центр давления расположен впереди центра тяжести. Видно, что в этом случае возникший момент не уменьшит угол отклонения, а наоборот—увеличит его и тем самым еще больше отклонит ракету от первоначальной траектории полета. Такая ракета неустойчива.
Насколько быстро ракета возвратится в состояние равновесия, зависит от расстояния е между центрами тяжести и давления. Величина е должна быть не меньше 0,5 D, однако лучше, если это расстояние равно диаметру корпуса ракеты. Для обеспечения устойчивости ракеты ее обычно снабжают стабилизаторами, которые смещают центр давления назад. Очевидно, запас устойчивости ракеты зависит от того, насколько правильно выбрана площадь поверхности стабилизаторов.
Примером стабилизатора может служить встречающийся в селах жестяной флюгер (например, в виде птицы, стрелы и т. д.), который всегда располагается острием к ветру (однако только потому, что умело выбраны форма и величины поверхностей впереди и сзади центра тяжести).
Каким на практике должно быть соотношение продольных поверхностей ракеты для выполнения условия устойчивости, показано на рис. 2.28. Полная длина ракеты в среднем должна составлять 16—20 D (где D—диаметр ракеты). Площадь поверхности стабилизаторов Р2=(0,8—1,0) Р1 (где Р1—площадь поверхности корпуса).

Мы рассмотрим два метода: расчетный и практический (путем вывешивания), позволяющие с достаточной точностью определить центр давления (размеры и форма модели ракеты схематически показаны на рис. 2.29).

При использовании расчетного метода вычерчивают в выбранном масштабе вид модели сбоку, определяют площади каждого элемента (т. е. головной части, корпуса и стабилизаторов) и дальнейший расчет проводят относительно выбранной точки, например передней точки головной части (вершины модели). На рисунке необходимо отметить центры тяжести всех геометрических фигур, образующих силуэт (контур) модели.
Поочередно рассчитывают площади всех поверхностей в мм2, начиная от головной части модели. Площади треугольников, прямоугольников и т. п. находят по известным из геометрии формулам. Например, для модели рис. 2.29 площадь треугольника (головной части) равна 40*30/2=600 мм2; площадь прямоугольника, соответствующая корпусу, составляет 170*30=5100 мм2. Площадь поверхности скошенной части стабилизатора равна 2*20*20/2=400 мм2, а его кормовой части 2*30*20= 1200 мм2. Умножая площадь поверхности на расстояние от вершины модели до центра тяжести соответствующей площади (на рис. 2.29 они обозначены точками), получим момент (мм2*мм). Сумма моментов, поделенная на суммарную площадь, даст местоположение геометрического центра контура, или центра давления модели.
Таким образом, для рассматриваемого случая получаем суммарную площадь 600+5100+400+1200=7300 мм2, моменты 600*25=15000 мм^мм, 5100*125=637500 мм2*мм, 400*173= =69200 мм2*мм, 1200*195=234000 мм2*мм и сумму моментов 15000+637500+69200+234000=955700 мм2*мм. Расстояние от центра давления до вершины модели ракеты равно
При использовании практического метода нужно вырезать из картона силуэт данной модели, лучше всего в натуральную величину. Путем уравновешивания находим центр тяжести этой плоской фигуры, который и будет искомым центром давления модели (рис. 2.30).

Для определения центра тяжести готовой модели ее нужно подвесить. Варьируя положение точки подвеса, можно достичь такого положения, при котором модель сохраняет равновесие

(рис. 2.31). В этой точке (точнее, в центре соответствующего сечения модели) и будет находиться ее центр тяжести. Однако для нас важно определить центр тяжести при проектировании модели, чтобы можно было правильно его расположить относительно центра давления (рис. 2.31, 2.32).

Любая модель ракеты состоит из нескольких частей, каждая из которых имеет свой центр тяжести. Зная массы отдельных частей и местоположение их центров тяжести, -можно при помощи простого расчета определить центр тяжести модели. Массу можно вычислить, взвешивая отдельные части или умножая их

объем на удельный вес(ПРИЛОЖЕНИЕ 1). Для определения центра тяжести модели нужно вычертить контур (рис. 2.33) проектируемой модели в произвольном масштабе и на рисунке выделить все составляющие части и их центры тяжести. Затем нужно вычислить моменты относительно передней (или задней) точки модели. Полученные моменты суммируют и делят полученную сумму на массу модели. В результате определяют искомое местоположение центра тяжести(ПРИЛОЖЕНИЕ 2). В рассматриваемом случае (табл. 2.2) центр тяжести находится на расстоянии 8331 г/мм / 77 г= 108,2 мм от вершины модели ракеты.
Таблица 2.2

Теперь можно определить расстояние между центрами тяжести и давления и проверить, выполняется ли основное соотношение, согласно которому это расстояние должно быть больше половины диаметра. В нашем примере имеем 130,9 —108,2 = 22,7 мм, т. е. 3/4 диаметра ракеты. Следовательно, условие устойчивости выполнено (в противном случае пришлось бы сделать более тяжелой головную часть или, что лучше, сконструировать более легкие стабилизаторы).
Неуправляемые ракеты, а таковыми в соответствии с правилами должны быть ракетные модели, летят по баллистическим траекториям (как брошенный камень или мяч), а не так, как летит

самолет, бумажный голубь или авиамодель с крыльями, создающими подъемную силу. Это основное различие проиллюстрировано на рис. 2.34.
Почти все модели, как и настоящие ракеты, оборудованы двигателями, расположенными позади центра тяжести (конечно, лучше было бы поместить их спереди—тогда не было бы трудностей с моментами). По этой причине линия действия тяги типичного кормового двигателя должна быть направлена вдоль оси симметрии модели и проходить через ее центр тяжести. Это требует большой точности при конструировании и сборке.
На стартующую модель вблизи поверхности земли может налететь боковой ветер, действуя на нее с некоторой силой, приложенной в центре давления. Так как скорость полета на начальном участке траектории мала, модель при этом может отклониться по направлению ветра (рис. 2.35).

Обычно на модели устанавливают 3 или 4 стабилизатора (иногда до 6), действующих как оперение стрелы, выпущенной

из лука. Большее количество стабилизаторов не оправдывает своего назначения, так как вследствие увеличения площади поперечного сечения значительно возрастает сопротивление. Количество стабилизаторов, их размер и форму определяют опытным путем. На практике принято считать, что хорда стабилизатора должна составлять от 1,5 до 2 диаметров модели. Часто используют кольцевые стабилизаторы, ширина которых в среднем равняется 0,5 диаметра кольца. Стабилизаторы этого типа эффективны при больших диаметрах кольца (не менее двух диаметров корпуса модели). Малые кольцевые стабилизаторы незначительно улучшают устойчивость модели. На рис. 2.36 показаны различные типы стабилизаторов. Там же приведены возможные формы головных обтекателей.
Приложения:
1. Вот удельный вес (г/см3) некоторых типичных материалов, используемых при конструировании моделей ракет: бальза — 0,15; сосна — 0,6; свинец — 11,4; латунь — 8,5; алюминий — 2,7; сталь — 7,75; картон — 1,1.
2. Центры тяжести различных геометрических фигур можно найти в справочниках, например, Кошкин Н. И., Ширкевич М. Г., Справочник по элементарной физике; В. Левин, Справочник конструктора точных приборов.